Sometimes one must solve the same optimization problem repeatedly, with only a small change in the parameters of the problem each time. Examples of this may include a robot which solves a motion planning problem for 10 seconds into the future, then takes an action, then resolves the problem 10ms later when the environment changes. Or an algorithmic trader, who recalculates the best predictor in a linear regression 100 times a second to take into account a small amount of new signal. Does is make sense to re-solve the optimization problem from scratch each time the trader, or the robot, wants to update its estimate? It certainly does not. However, knowledge of how to create solvers which are faster in successive solves of the same problem is very limited.
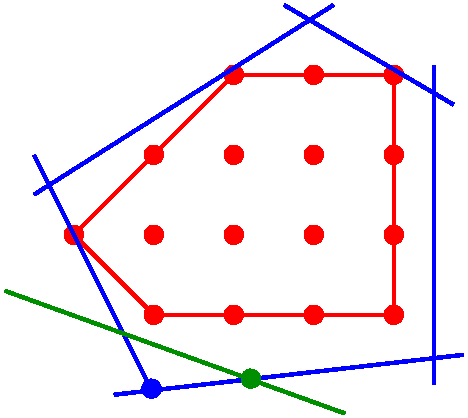
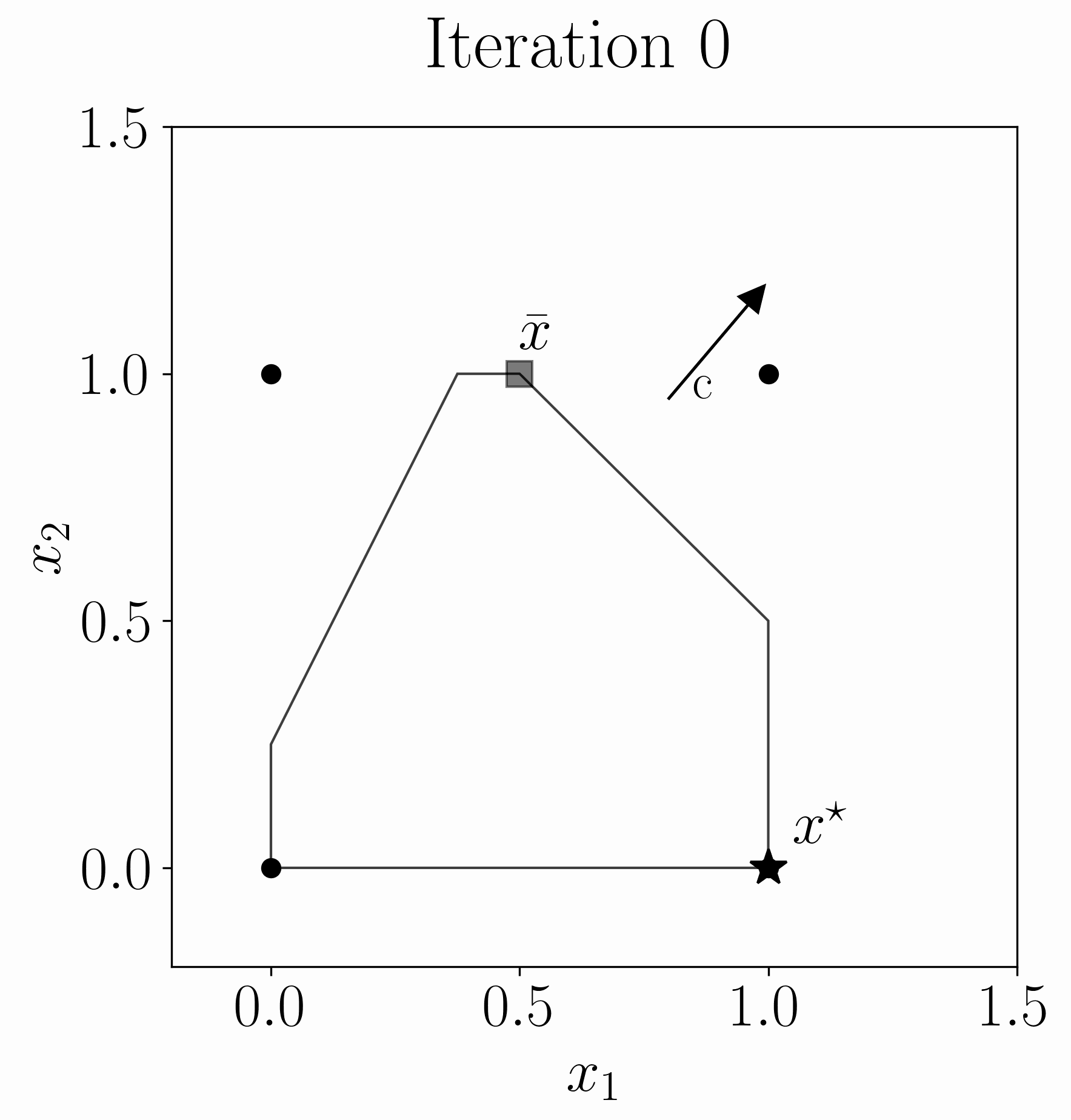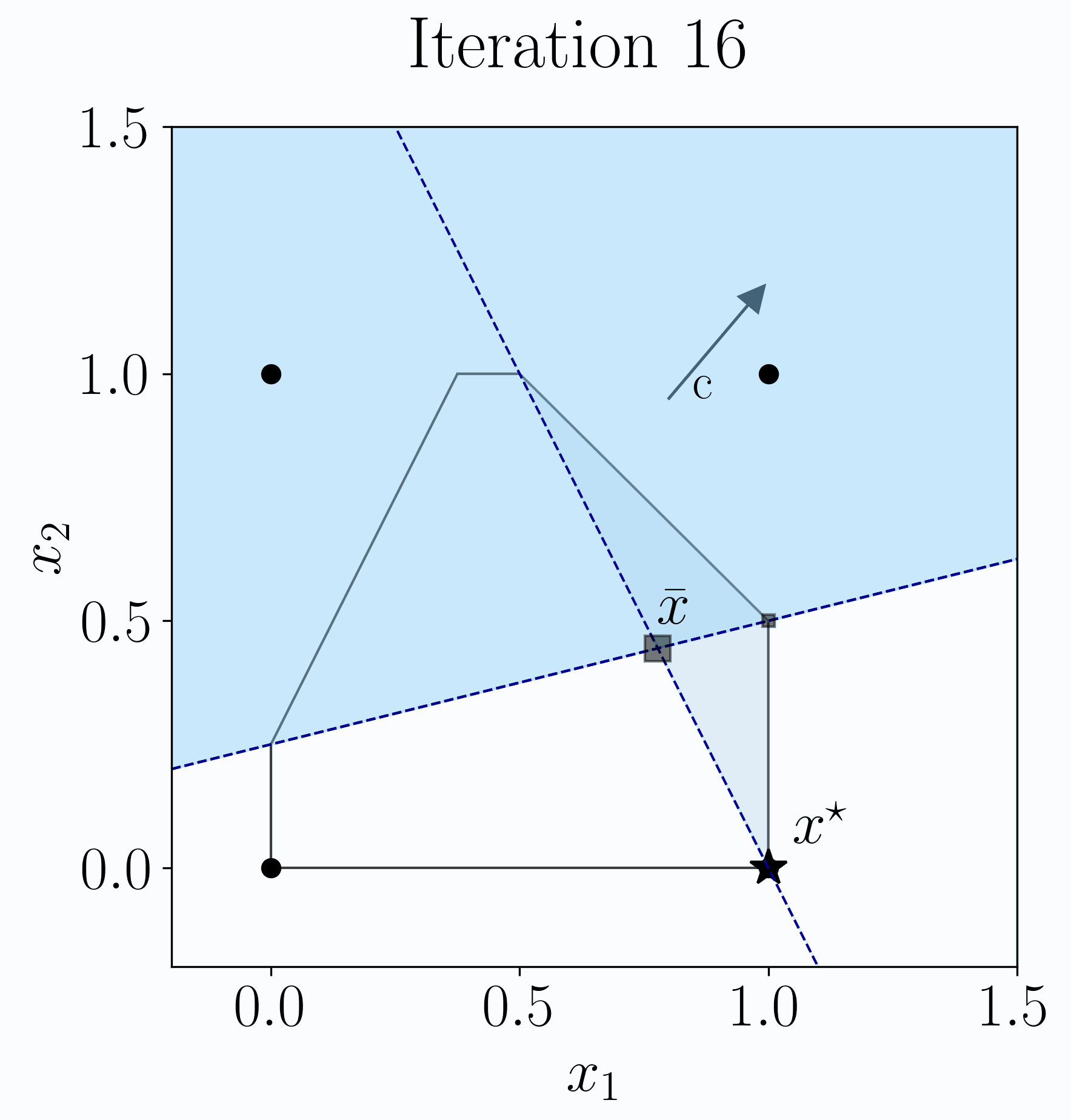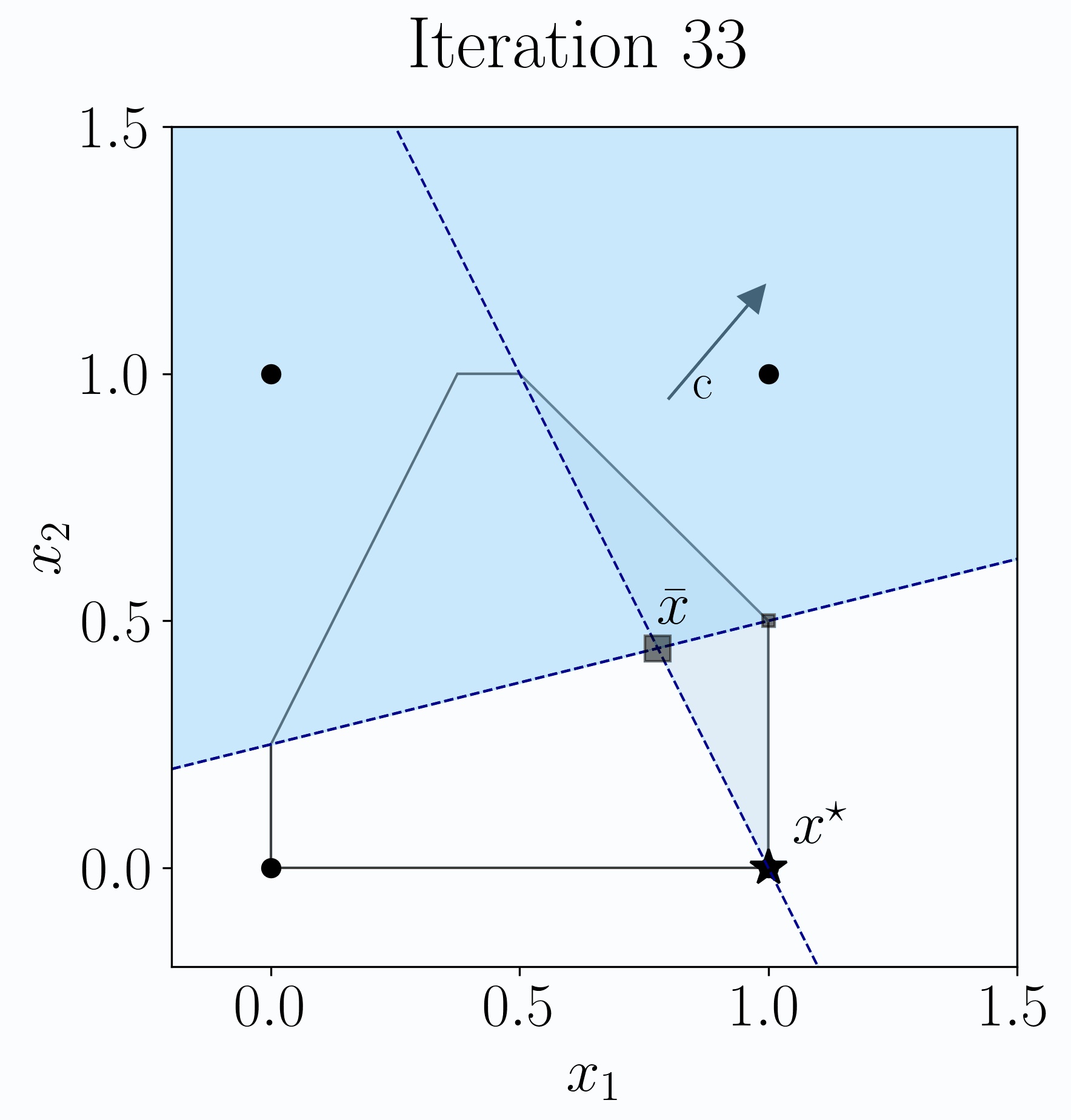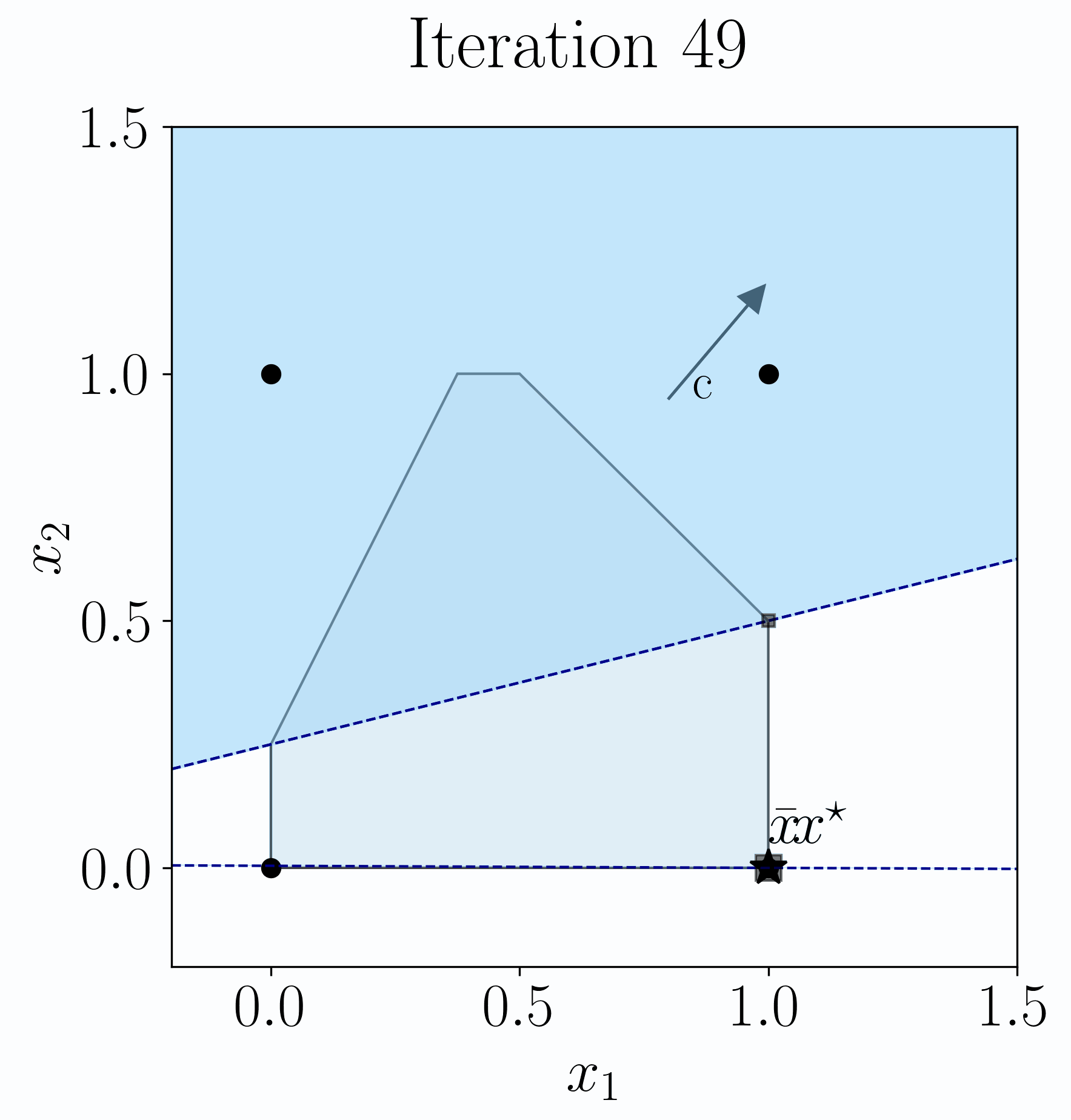
In this paper, we contribute new technology to help solve this problem in the case of Mixed Integer Programs (MIPs) using cutting planes. Cutting planes are used in all state-of-the-art MIP solvers. They are cuts (inequalities) which cut off part of the linear relaxation of the feasible region, without cutting off any integer-feasible points.
Left: An illustration of a cutting plane. The blue represents the continuous relaxation of the feasible set and the received dots represent the feasible integer points. The green line represents a cutting plane. It cuts off some of the continuous relaxation in such a way that it does not cut off any feasible integer points, so optimizing a function over all integers in the set will return same objective value.
We use Cut-Generating Linear Programs (CGLPS) to create a differentiable parametric representation for a family of cutting planes for a given MIP and propose a reinforcement-learning architecture to learn how to generate the most effective cuts for a given parameter. Our trained reinforcement learning agent is able to generate stronger cuts for sequences of problems which it is trained on than many standard cutting-plane generation methods.
Left: An example of an integer program. The continuous relaxation is represented by the polyhedron in the interior of the square. The integer points are the black circles. Our method involves creating a differentiable parametrization for cutting planes, meaning that we can continuously move between cuts, as shown in the gif. This allows us to use a machine learning-algorithm to optimize over the cuts. As you can see, as the number of training iterations increases, the cutting plane cuts off a larger area of the feasible region.
Abstract: We consider the problem of solving a family of parametric mixed-integer linear optimization problems where some entries in the input data change. We introduce the concept of cutting-plane layer (CPL), i.e., a differentiable cutting-plane generator mapping the problem data and previous iterates to cutting planes. We propose a CPL implementation to generate split cuts, and by combining several CPLs, we devise a differentiable cutting-plane algorithm that exploits the repeated nature of parametric instances. In an offline phase, we train our algorithm by updating the internal parameters controlling the CPLs, thus altering cut generation. Once trained, our algorithm computes, with predictable execution times and a fixed number of cuts, solutions with low integrality gaps. Preliminary computational tests show that our algorithm generalizes on unseen instances and captures underlying parametric structures.